2020贵州中烟工业公司招聘考试行测备考：八卦排列组合那些事儿

在历年来的公务员考试中排列组合是一个高频考点，几乎每年都会出现。但是在学生中排列组合是一个难点不易得分，因为排列和组合应用起来很困难，今天我们就一起来八卦一下排列组合的那些事。

　　排列与组合的共同点是从n个不同的元素中，任取m(m≤n)个元素，而不同点是排列是按照一定的顺序排成一列，组合是无论怎样的顺序并成一组，因此“有序”与“无序”是区别排列与组合的重要标志。

　　下面通过实例来体会排列与组合的区别。

　　【例】甲、乙、丙、丁四个人，选2人去参加比赛，问一共有( )种选法?

　　A. 5B. 6

　　C. 7D. 8

　　【答案】B

　　

　　【例】甲、乙、丙三个人到旅店住店，旅店里只有三个房间，恰好每个房间住一个人，问一共有( )种住法。

　　A. 5B. 6

　　C. 7D. 8

　　【答案】B

　　【解题思路】解法一：三个房间三个人，把房间固定，给甲乙丙三人排队(有顺序，故用排列)，一种排法就对应一种住法，所以共有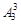=6种住法。因此，选择B选项。

　　解法二：先安排甲，3种选法;再安排乙，有2种选法;最后安排丙，只1种选法。共有住法3×2×1=6种。因此，选择B选项。

　　解密排列组合的中的多步运行

　　加法原理：若完成一件事，可以根据某个条件分为几种情况，各种情况都能独立完成任务，则将多种情况计算出的结果相加，所得的和为完成这件事的种类数。

　　乘法原理：若完成一件事，需要划分成多个步骤依次完成，每个步骤内的任务之间没有交叉，则将每个步骤计算出的结果相乘，所得的积为完成这件事的种类数。

　　加法原理和乘法原理的区别：

　　一个与分类有关，一个与分步有关;加法原理是 “分类完成”，乘法原理是 “分步完成”。

　　【例】(2018-广州324-53.)某部门开展年终评选工作。需从11名员工评选出一名优秀员工和两名积极员工。且优秀员工与积极员工不能为同一人。则可能会出现的评选结果共有( )种。

　　A. 495B. 990

　　C. 1210D. 1980

　　【答案】A

　　【解题思路】

　　第一步，题干要求“优秀员工与积极员工不能为同一人”，采用分步计算的方法。

　　第二步，先从11名员工中选出1人作为优秀员工，为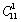;再从剩余的10人中选出2人作为积极员工，为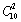，所以共有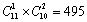种评选结果。因此，选择A选项。

　　【例】(2018-广西-54.)单位3个科室分别有7名、9名和6名职工。现抽调2名来自不同科室的职工参加调研活动，问有多少种不同的挑选方式?

　　A. 146B. 159

　　C. 179D. 286

　　【答案】B

　　【解题思路】

　　第一步，本题考查排列组合问题，采用分类的方法解题。

　　第二步，设3个科室分别为A、B、C科室，那么挑两个科室、每个科室挑1人的情况如下：

　　①从A、B里挑，有7×9=63种方式;

　　②从B、C里挑，有9×6=54种方式;

　　③从A、C里挑，有7×6=42种方式。

　　第三步，共有63+54+42=159种方式(可使用尾数法)。因此，选择B选项。

　　以上就是排列组合的基本知识要点，是学生掌握排列组合的基本解题技巧，今天我们就先八卦排列组合的基本家庭组成，下次我们一起八卦排列组合的特殊小题型，也就是它的成长变形记呦，在八卦的路上我们一起加油吧!!!