已知直角三角形ABC,其中∠ABC=60°,∠C=90°,AB=2,求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积.

答案 : 如图以斜边AB为轴旋转一周,得旋转体是以AB边的高CO为底面半径的两个圆锥组成的组合体
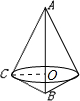 ∵AB=2,CB=1,∠B=60°
∵AB=2,CB=1,∠B=60°∴CB=sin30°•AB=1,CA=cos30°•AB=
| 3 |
CO=
| AC•CB |
| AB |
|
||
| 2 |
故此旋转体的表面积,S=π×OC×AC+π×OC×BC=π×
|
||
| 2 |
| 3 |
3+
|
||
| 2 |
故此旋转体的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 4 |
| π |
| 2 |
编辑推荐:
下载Word文档

温馨提示:因考试政策、内容不断变化与调整,长理培训网站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准! (责任编辑:长理培训)






















点击加载更多评论>>