MBA联考数学基础知识重点汇总（二）

（四）二元一次方程

定义：把两个含有不同未知数的一次方程联合在一起，那么这两个方程就组成了一个二元一次方程组。
有几个方程组成的一组方程叫做方程组。如果方程组中含有两个未知数，且含未知数的项的次数都是一次，那么这样的方程组叫做二元一次方程组

二元一次方程组的解法：

方法一　加减消元法

用加减法消元的一般步骤为：

①在二元一次方程组中，若有同一个未知数的系数相同（或互为相反数），则可直接相减（或相加），消去一个未知数；

②在二元一次方程组中，若不存在①中的情况，可选择一个适当的数去乘方程的两边，使其中一个未知数的系数相同（或互为相反数），再把方程两边分别相减（或相加），消去一个未知数，得到一元一次方程；
③解这个一元一次方程；

④将求出的一元一次方程的解代入原方程组系数比较简单的方程，求另一个未知数的值；

⑤把求得的两个未知数的值用大括号联立起来，这就是二元一次方程组的解。

方法二　代入消元法

用代入消元法的一般步骤是：

①选一个系数比较简单的方程进行变形，变成 y = ax +b 或 x = ay + b的形式；

②将y = ax + b 或 x = ay + b代入另一个方程，消去一个未知数，从而将另一个方程变成一元一次方程；
③解这个一元一次方程，求出 x 或 y 值；

④将已求出的 x 或 y 值代入方程组中的任意一个方程（y = ax +b 或 x = ay + b），求出另一个未知数；

⑤把求得的两个未知数的值用大括号联立起来，这就是二元一次方程的解。

（五）数列

定义：依一定次序排列的一列数叫做数列。数列中的每一个数都叫这个数列的项。

数列一般的表达形式：
a1，a2，a3，…，an，… 或简记为{an}
其中an叫做数列{an} 的通项，自然数n 叫做an的序号。如果通项an与n之间的函数关系，可以用一个关于n 的解析式f(n)表达，则称an=f(n)为数列{an}的通项公式。

如数列1,1/2，1/4，1/8，…的一个通项公式为an=1/2^ (n-1)

知道了一个数列的通项公式，就等于从整体上掌握了这个数列，即由通项公式可求出这个数列中的任意一项；对任意给出的数可以确定它是否是该数列中的项。

如在上面给出的数列中，由an=1/2^(n-1)，可以求出a11=1/2^10=1/1024, 也可以断定1/10不是该数列中的项，而由1/64=1/2^6得n=7，即1/64是已知数列中的第7项。

数列的前n项的和记做Sn。对于数列忆{an} ，显然有Sn= a1+a2+a3+…+an
当n=1 时，a1=S1，当n大于等于2 时，an=Sn-S（n-1）
项数有限的数列叫做有穷数列，项数无限的数列叫做无穷数列。

等差数列 ：

定义：如果一个数列从第2 项起，每一项与它前一项的差等于同一个常数，这个数列就叫做等差数列. 这个常数叫做这个等差数列的公差，记做d。

即{an}是等差数列<=>a（n+1）－an=d (常数) ，d 为等差数列{an}的公差。

等差数列的一般表达形式为：a1. ，a1+d，a1 +2d，…，a1+(n 一1)d，…

1.等差中项： 如果a， A，b成等差数列，则A 叫做a与b的等差中项，且A=（a+b）/2

2.通项公式
an=a1+（n－1）d

3. 前n 项和公式：
Sn=n（a1+an）/2
Sn=na1+[n（n－1）/2]d

1. 常数列c,c,…，c，…是公差d=0的等差数列。

2. 若Sn是等差数{an}的前n项和，则sn，S2n－Sn，S3n－S2n，…仍成等差数列

等比数列：

定义：如果一个数列从第二项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫作等比数列，这个常数叫作等比数列的公比，用字母q表示（q≠ 0）。

1.等比中项：如果在a与b之间插入一个数G，使a、G、b成等比数列，那么G叫作a与b的等比中项（两个符号相同的非零实数，都有两个等比中项）

2.通项公式：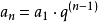

3.前n项和公式：当q≠1时，或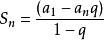

（六）充要条件

（1）先看“充分条件和必要条件”

当命题“若p则q”为真时，可表示为p => q，则我们称p为q的充分条件，q是p的必要条件。这里由p => q，得出p为q的充分条件是容易理解的。

但为什么说q是p的必要条件呢?

事实上，与“p => q”等价的逆否命题是“非q => 非p”。它的意思是：若q不成立，则p一定不成立。这就是说，q对于p是必不可少的，因而是必要的。

（2）再看“充要条件”

若有p =>q，同时q => p,则p既是q的充分条件，又是必要条件。简称为p是q的充要条件。记作p<=>q

回忆一下初中学过的“等价于”这一概念；如果从命题A成立可以推出命题B成立，反过来，从命题B成立也可以推出命题A成立，那么称A等价于B，记作A<=>B。“充要条件”的含义，实际上与“等价于”的含义完全相同。也就是说，如果命题A等价于命题B，那么我们说命题A成立的充要条件是命题B成立；同时有命题B成立的充要条件是命题A成立。

（3）定义与充要条件

数学中，只有A是B的充要条件时，才用A去定义B，因此每个定义中都包含一个充要条件。如“两组对边分别平行的四边形叫做平行四边形”这一定义就是说，一个四边形为平行四边形的充要条件是它的两组对边分别平行。

显然，一个定理如果有逆定理，那么定理、逆定理合在一起，可以用一个含有充要条件的语句来表示。

“充要条件”有时还可以改用“当且仅当”来表示，其中“当”表示“充分”。“仅当”表示“必要”。

（4）一般地，定义中的条件都是充要条件，判定定理中的条件都是充分条件，性质定理中的“结论”都可作为必要条件。