2020军队文职人员招聘数学3知识点：圆的位置关系经典例题

圆的位置关系经典例题

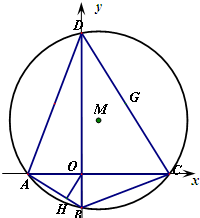
如图，在平面直角坐标系中，方程为x²+y²+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直，且AC和BD分别在x轴和y轴上．
（1）求证：F＜0；
（2）若四边形ABCD的面积为8，对角线AC的长为2，且

AB

•

AD

=0，求D²+E²-4F的值；
（3）设四边形ABCD的一条边CD的中点为G，OH⊥AB且垂足为H．试用平面解析几何的研究方法判断点O、G、H是否共线，并说明理由．

答案 : （1）证法一：由题意，原点O必定在圆M内，即点（0，0）代入方程x²+y²+Dx+Ey+F=0的左边后的值小于0，
于是有F＜0，即证．…（4分）
证法二：由题意，不难发现A、C两点分别在x轴正负半轴上．设两点坐标分别为
A（a，0），C（c，0），则有ac＜0．
对于圆方程x²+y²+Dx+Ey+F=0，当y=0时，可得x²+Dx+F=0，其中方程的两根分别为点A和点C的横坐标，于是有x_Ax_C=ac=F．
因为ac＜0，故F＜0．…（4分）
（2）不难发现，对角线互相垂直的四边形ABCD面积S=

|AC|•|BD|

2

，因为S=8，|AC|=2，可得|BD|=8．…（6分）
又因为

AB

•

AD

=0，所以∠A为直角，而因为四边形是圆M的内接四边形，故|BD|=2r=8⇒r=4．…（8分）
对于方程x²+y²+Dx+Ey+F=0所表示的圆，可知

D2

4

+

E2

4

-F=r2，所以D²+E²-4F=4r²=64．…（10分）
（3）证：设四边形四个顶点的坐标分别为A（a，0），B（0，b），C（c，0），D（0，d）．
则可得点G的坐标为(

c

2

，

d

2

)，即

OG

=(

c

2

，

d

2

)．…（12分）
又

AB

=(-A，B)，且AB⊥OH，故要使G、O、H三点共线，只需证

AB

•

OG

=0即可．
而

AB

•

OG

=

bd-ac

2

，且对于圆M的一般方程x²+y²+Dx+Ey+F=0，
当y=0时可得x²+Dx+F=0，其中方程的两根分别为点A和点C的横坐标，
于是有x_Ax_C=ac=F．…（14分）
同理，当x=0时，可得y²+Ey+F=0，其中方程的两根分别为点B和点D的纵坐标，于是有y_By_D=bd=F．
所以，

AB

•

OG

=

bd-ac

2

=0，即AB⊥OG．
故O、G、H必定三点共线．…（16分）