不属于矩阵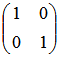的特征向量是()。

设λ=-2是可逆矩阵A的特征值，则矩阵A-1+A有一特征值()。

　　A

　　B

　　C0

　　D

实二次型为正定二次型的充要条件是()。

　　A负惯性指数全为零

　　B对任意向量，都是xTAx>0

　　C|A|>0

　　D存在n阶矩阵P，使A=PTP

实二次型的符号差为()。

　　A0

　　B1

　　C2

　　D3

实二次型的秩为3，符号差为-1，则f的标准形可能为()。 A

　　B

　　C

　　D

实对称矩阵A的秩等于r，又它有m个正特征值.则它的符号差为()。

　　Ar

　　Bm-r

　　C2m-r

　　Dr-m

二次型的标准形为()。 A

　　B

　　C

　　D

二次型f=xTAx经过满秩线性变换x=Py可化为yTBy，则矩阵A与B()。

　　A一定合同

　　B一定相似

　　C即相似又合同

　　D即不相似也不合同

若矩阵A与B是合同的，则它们也是()。

　　A相似

　　B相等

　　C等价

　　D满秩

二次型的秩为()。

　　A1

　　B2

　　C3

　　D4

设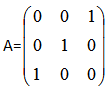，则以矩阵A为对应的二次型是()。

　　A

　　B

　　C

　　D