2018年成人高考《数学（文）》章节难点习题(10)

 　　●歼灭难点训练

　　一、选择题

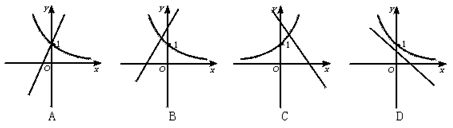
　　1.(★★★★)当a≠0时，y=ax+b和y=bax的图象只可能是( )

 

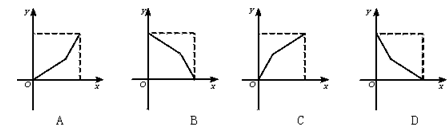
　　2.(★★★★)某学生离家去学校，由于怕迟到，所以一开始就跑步，等跑累了，再走余下的路，下图中y轴表示离学校的距离，x轴表示出发后的时间，则适合题意的图形是( )

 

　　二、填空题

　　3.(★★★★★)已知函数f(x)=log2(x+1)，将y=f(x)的图象向左平移1个单位，再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)，得到函数y=g(x)的图象，则函数F(x)=f(x)-g(x)的最大值为_________.

　　三、解答题

　　4.(★★★★)如图，在函数y=lgx的图象上有A、B、C三点，它们的横坐标分别为m,m+2,m+4(m>1).

　　(1)若△ABC面积为S，求S=f(m);

　　(2)判断S=f(m)的增减性.

 

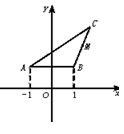
　　5.(★★★★)如图，函数y= |x|在x∈[-1,1]的图象上有两点A、B，AB∥Ox轴，点M(1，m)(m∈R且m> )是△ABC的BC边的中点.

　　(1)写出用B点横坐标t表示△ABC面积S的函数解析式S=f(t);

　　(2)求函数S=f(t)的最大值，并求出相应的C点坐标.

 

　　6.(★★★★★)已知函数f(x)是y= -1(x∈R)的反函数，函数g(x)的图象与函数y=- 的图象关于y轴对称，设F(x)=f(x)+g(x).

　　(1)求函数F(x)的解析式及定义域;

　　(2)试问在函数F(x)的图象上是否存在两个不同的点A、B，使直线AB恰好与y轴垂直?若存在，求出A、B的坐标;若不存在，说明理由.

　　7.(★★★★★)已知函数f1(x)= ,f2(x)=x+2,

　　(1)设y=f(x)= ，试画出y=f(x)的图象并求y=f(x)的曲线绕x轴旋转一周所得几何体的表面积;

　　(2)若方程f1(x+a)=f2(x)有两个不等的实根，求实数a的范围.

　　(3)若f1(x)>f2(x-b)的解集为[-1， ]，求b的值.

　　8.(★★★★★)设函数f(x)=x+ 的图象为C1，C1关于点A(2，1)对称的图象为C2，C2对应的函数为g(x).

　　(1)求g(x)的解析表达式;

　　(2)若直线y=b与C2只有一个交点，求b的值，并求出交点坐标;

　　(3)解不等式logag(x)

　　参考答案

　　难点磁场

　　解法一：观察f(x)的图象，可知函数f(x)的图象过原点，即f(0)=0,得d=0,又f(x)的图象过(1，0)，∴f(x)=a+b+c①,又有f(-1)<0,即-a+b-c<0②,①+②得b<0,故b的范围是(-∞,0)

　　解法二：如图f(0)=0有三根，∴f(x)=ax3+bx2+cx+d=ax(x-1)(x-2)=ax3-3ax2+2ax,∴b=

　　-3a,∵a>0,∴b<0.

　　歼灭难点训练

　　一、1.解析：∵y=bax=(ba)x,∴这是以ba为底的指数函数.仔细观察题目中的直线方程可知：在选择支B中a>0,b>1,∴ba>1,C中a<0,b>1,∴0

　　答案：A

　　2.解析：由题意可知，当x=0时，y最大，所以排除A、C.又一开始跑步，所以直线随着x的增大而急剧下降.

　　答案：D

 

　　二、3.解析：g(x)=2log2(x+2)(x>-2)

　　F(x)=f(x)-g(x)=log2(x+1)-2log2(x+2)

　　=log2 ∵x+1>0,∴F(x)≤ =-2

　　当且仅当x+1= ,即x=0时取等号.

　　∴F(x)max=F(0)=-2.

　　答案：-2

　　三、4.解：(1)S△ABC=S梯形AA′B′B+S梯形BB′C′C-S梯形AA′C′C.

　　(2)S=f(m)为减函数.

　　5.解：(1)依题意，设B(t, t),A(-t, t)(t>0),C(x0,y0).

　　∵M是BC的中点.∴ =1, =m.

　　∴x0=2-t,y0=2m- t.在△ABC中，|AB|=2t,AB边上的高hAB=y0- t=2m-3t.

　　∴S= |AB|·hAB= ·2t·(2m-3t),即f(t)=-3t2+2mt,t∈(0,1).

　　(2)∵S=-3t2+2mt=-3(t- )2+ ,t∈(0,1 ,若 ，即 

　　6.解：(1)y= -1的反函数为f(x)=lg (-1

　　由已知得g(x)= ,∴F(x)=lg + ,定义域为(-1，1).

　　(2)用定义可证明函数u= =-1+ 是(-1，1)上的减函数，且y=lgu是增函数.∴f(x)是(-1，1)上的减函数，故不存在符合条件的点A、B.

　　7.解：(1)y=f(x)= .图略.

　　y=f(x)的曲线绕x轴旋转一周所得几何体的表面积为(2+ )π.

　　(2)当f1(x+a)=f2(x)有两个不等实根时，a的取值范围为2-

　　(3)若f1(x)>f2(x-b)的解集为[-1， ]，则可解得b= .

　　8.(1)g(x)=x-2+ .(2)b=4时，交点为(5，4);b=0时，交点为(3，0).

　　(3)不等式的解集为{x|4