代入排除法就是从题目的选项入手,代入选项后,如果不符合已知的条件,或者推出矛盾,则可排除此选项的方法。在公务员考试中,行测全部都是单项选择题,代入排除法是应对选择题最有效的方法。
使用代入排除是,我们需要注意以下几点:
1.四个选项,只有一个是正确的,所以只要有一项满足题目的所有条件,这个选项就是正确答案。
2.一个选项只要不满足题目中的其中一个条件,它就不是答案。
下面我们就通过公务员考试的一些真题来带大家感受一下代入排除法的妙处。
【例1】两个数的差是2345,两数相除的商是8,这两个数之和为( )。
A.2353 B.2896 C.3015 D.3456
【解析】由两个数的差是2345可知,这两个数必是一奇一偶,则两个数的和为奇数,可排除B、D两项;又由两数相除的商是8可知,一个数是另一个数的8倍,则两个数的和是较小数的9倍,即两个数的和是9的倍数,排除A,选择C。
【例2】一个袋子里放着各种颜色的小球,其中红色球占1/4,后来又往袋子里放了10个红球,这时红球占总数的1/2,问原来袋子里有多少个球?( )
A.8 B.12 C.16 D.20
【解析】直接代入,发现只有D满足条件。
【例3】三位专家为10幅作品投票,每位专家分别都投出了5票,并且每幅作品都有专家投票。如果三位专家都投票的作品列为A等,两位专家投票的作品列为B等,仅有一位专家投票的作品列为C等。则下面说法正确的是( )
A、A等与B等共6幅 B、B等和C等共7幅
C、A最多有5幅 D、A等比C等少5幅
【解析】设A等作品有x幅,B等作品有y幅,C等作品有z幅,则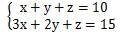
(要求x、y、z都为正整数),这也是非常典型的不定方程组问题。对于这样的问题,我们可以采用代入排除法。
(1)代入A选项,即x+y=6,则z=4,又因为3x+2y+z﹥2(x+y)+z,代入即可得到3x+2y+z﹥16,与原方程3x+2y+z=15矛盾,排除。
(2)代入B选项,即y+z=7,则x=3,又因为3x+2y+z﹥3x+(y+z),代入即可得到3x+2y+z﹥16,与原方程3x+2y+z=15矛盾,排除。
(3)代入C选项,若x=5,则3x+2y+z﹥3x,代入即可得到3x+2y+z﹥16,与原方程3x+2y+z=15矛盾,排除。
A、B、C都排除,所以选D。
总结:本题主要使用代入排除法来解不定方程,看似复杂,其实心算即可快速得出正确答案。
【例4】甲、乙、丙三人来自学校足球队、乒乓球队、篮球队。下列说法只有一种对的:(1)甲是足球队的;(2)乙不是足球队的;(3)丙不是篮球队的。甲、乙、丙三人分别是哪一个队的( )
A. 甲是足球队的;乙是篮球队的;丙是乒乓球队的
B. 甲是篮球队的;乙是足球队的;丙是乒乓球队的
C. 甲是乒乓球队的;乙是足球队的;丙是篮球队的
D. 甲是乒乓球队的;乙是篮球队的;丙是足球队的
【解析】本题目若采用常规假设,所花费的时间较多,若从选项入手较为快速准确。若A正确,则(1)(2)(3)都为真,与题干“下列说法只有一种对的”矛盾,排除A,若B正确,则(1)(2)为假,(3)为真,满足题干信息,所以选择B。
经过验证,若C选项正确(1)(2)(3)都为假,D选项正确则(1)为假(2)(3)为真,与题干矛盾,因此C.D都为错误选项。正确答案选择【B】
【例5】甲、乙、丙均为教师,其中一位是大学教师,一位是中学教师,一位是小学教师。并且大学教师比甲的学历高,乙的学历与小学教师不同,小学老师的学历比丙的低。
由此可以推出( )。
A.甲是小学教师,乙是中学教师,丙是大学教师
B.甲是中学教师,乙是小学教师,丙是大学教师
C.甲是大学教师,乙是小学教师,丙是中学教师
D.甲是大学教师,乙是中学教师,丙是小学教师
【解析】A。首先根据题干信息可知,题干涉及了人物(甲、乙、丙)和职务(大学教师、中学教师、小学教师)两类元素,且四个选项都是对人物与职务关系的判断,根据题干信息,直接采用排除法。根据“乙的学历与小学教师不同,小学老师的学历比丙的低”可知,乙和丙不是小学教师,那么,甲一定是小学老师。因此排除 B、C、D、三项。故答案选择A项。
通过以上几道题目可以发现,代入排除法不仅适用于数学运算,还适用于逻辑判断。需要进一步明确的是,代入排除法适用于行测的各个模块,不要局限于数学运算。
使用代入排除是,我们需要注意以下几点:
1.四个选项,只有一个是正确的,所以只要有一项满足题目的所有条件,这个选项就是正确答案。
2.一个选项只要不满足题目中的其中一个条件,它就不是答案。
下面我们就通过公务员考试的一些真题来带大家感受一下代入排除法的妙处。
【例1】两个数的差是2345,两数相除的商是8,这两个数之和为( )。
A.2353 B.2896 C.3015 D.3456
【解析】由两个数的差是2345可知,这两个数必是一奇一偶,则两个数的和为奇数,可排除B、D两项;又由两数相除的商是8可知,一个数是另一个数的8倍,则两个数的和是较小数的9倍,即两个数的和是9的倍数,排除A,选择C。
【例2】一个袋子里放着各种颜色的小球,其中红色球占1/4,后来又往袋子里放了10个红球,这时红球占总数的1/2,问原来袋子里有多少个球?( )
A.8 B.12 C.16 D.20
【解析】直接代入,发现只有D满足条件。
【例3】三位专家为10幅作品投票,每位专家分别都投出了5票,并且每幅作品都有专家投票。如果三位专家都投票的作品列为A等,两位专家投票的作品列为B等,仅有一位专家投票的作品列为C等。则下面说法正确的是( )
A、A等与B等共6幅 B、B等和C等共7幅
C、A最多有5幅 D、A等比C等少5幅
【解析】设A等作品有x幅,B等作品有y幅,C等作品有z幅,则
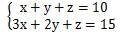
(要求x、y、z都为正整数),这也是非常典型的不定方程组问题。对于这样的问题,我们可以采用代入排除法。
(1)代入A选项,即x+y=6,则z=4,又因为3x+2y+z﹥2(x+y)+z,代入即可得到3x+2y+z﹥16,与原方程3x+2y+z=15矛盾,排除。
(2)代入B选项,即y+z=7,则x=3,又因为3x+2y+z﹥3x+(y+z),代入即可得到3x+2y+z﹥16,与原方程3x+2y+z=15矛盾,排除。
(3)代入C选项,若x=5,则3x+2y+z﹥3x,代入即可得到3x+2y+z﹥16,与原方程3x+2y+z=15矛盾,排除。
A、B、C都排除,所以选D。
总结:本题主要使用代入排除法来解不定方程,看似复杂,其实心算即可快速得出正确答案。
【例4】甲、乙、丙三人来自学校足球队、乒乓球队、篮球队。下列说法只有一种对的:(1)甲是足球队的;(2)乙不是足球队的;(3)丙不是篮球队的。甲、乙、丙三人分别是哪一个队的( )
A. 甲是足球队的;乙是篮球队的;丙是乒乓球队的
B. 甲是篮球队的;乙是足球队的;丙是乒乓球队的
C. 甲是乒乓球队的;乙是足球队的;丙是篮球队的
D. 甲是乒乓球队的;乙是篮球队的;丙是足球队的
【解析】本题目若采用常规假设,所花费的时间较多,若从选项入手较为快速准确。若A正确,则(1)(2)(3)都为真,与题干“下列说法只有一种对的”矛盾,排除A,若B正确,则(1)(2)为假,(3)为真,满足题干信息,所以选择B。
经过验证,若C选项正确(1)(2)(3)都为假,D选项正确则(1)为假(2)(3)为真,与题干矛盾,因此C.D都为错误选项。正确答案选择【B】
【例5】甲、乙、丙均为教师,其中一位是大学教师,一位是中学教师,一位是小学教师。并且大学教师比甲的学历高,乙的学历与小学教师不同,小学老师的学历比丙的低。
由此可以推出( )。
A.甲是小学教师,乙是中学教师,丙是大学教师
B.甲是中学教师,乙是小学教师,丙是大学教师
C.甲是大学教师,乙是小学教师,丙是中学教师
D.甲是大学教师,乙是中学教师,丙是小学教师
【解析】A。首先根据题干信息可知,题干涉及了人物(甲、乙、丙)和职务(大学教师、中学教师、小学教师)两类元素,且四个选项都是对人物与职务关系的判断,根据题干信息,直接采用排除法。根据“乙的学历与小学教师不同,小学老师的学历比丙的低”可知,乙和丙不是小学教师,那么,甲一定是小学老师。因此排除 B、C、D、三项。故答案选择A项。
通过以上几道题目可以发现,代入排除法不仅适用于数学运算,还适用于逻辑判断。需要进一步明确的是,代入排除法适用于行测的各个模块,不要局限于数学运算。
温馨提示:因考试政策、内容不断变化与调整,长职理培网站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准! (责任编辑:长职理培)






















点击加载更多评论>>