第66题 某次考试有一道多项选择题,共有A、B、C三个选项。参加考试的人中,共有20人选了A,15人选了B,10人选了C。其中选了两个选项的有5人,选了三个选项的有3人,还有2人未答此题。问有多少人参加考试?
A. 30
B. 34
C. 36
D. 40
【正确答案】:C
试题解析:
选两个选项的被重复计算了1次,选三个选项的被重复计算了2次,因此答这道题的有20+15+10-5-2×3=34人.共有34+2=36人参加考试。
第67题 某工厂男女职工比例原为19:12,后来新加入一些女职工,使得男女比例变为20:13,后来又加入了若干男职工,此时男女比例变为30:19。若最终加入的男职工比女职工多3人,那么最终工厂有多少人?
A. 686
B. 637
C. 720
D. 764
【正确答案】:B
试题解析:
第一次男职工人数没有发生变化,因此原男女职工比例为19:12=(19×20):(12×20)=380:240,加入女职工后,男女比例为20:13=(20×19):(13×19)=380:247,女职工增加了7份。第二次女职工没有发生变化,最终男女职工比例为30:19=(30×13):(19×13)=390:247.男职工增加了390-380=10份,男职工比女职工多增加了10-7=3份.对应3人.因此1份为1人。最终工厂人数应为390+247=637人。
第68题 小张去市场上出售工艺品,每件的定价恰好和工艺品件数相等,卖出若干件后,决定提价50%出售.最后共卖得125元。问小张有多少件工艺品?
A. 9
B. 10
C. 11
D. 12
【正确答案】:B
试题解析:
设小张有m件工艺品,定价为每件m元,卖出n件后,余下工艺品售价为m×(1+50%)=
化简得m(3m-n)=250,250=1×250=2×125=5×50=10×25,m、n为正整数,且m>n.由此可确定m=10,n=5。所以小张有10件工艺品。
第69题 一艘小船逆水而行,到A地时随身带的一个重要的水壶掉入水中随波而下。半小时后船行到B地.发现丢失了水壶,立即返回寻找,终于在距离A地5千米的地方追上水壶,然后又用了10分钟返回到A地。若小船从B地顺水行到A地需用时多少分钟?
A. 20
B. 22.5
C. 25
D. 27.5
【正确答案】:B
试题解析:
从A地到B地,小船与水壶速度和为静水中的船速,时间为半小时,那么,小船从B地到追上水壶,其速度差为静水中的船速。故时间也为半小时。此时,水壶已经漂流了0.5+0.5=1小时,水壶漂流的路程为5千米.所以水壶漂流的速度为每小时5千米,即水的流速为5千米/小时。船从追上水壶到返回A地,用了10分钟.即船逆水行5千米用10分钟,逆水航行的速度为5÷(10+60)=30千米/小时,那么静水中的船速为30+5=35千米/小时。A、B两地之间的距离为30×0.5=15千米。从B顺水到A,需要15+(35+5)×60=22.5分钟,或
第70题 某公司销售A、B、C三种产品,2010年度总销售业绩同比实现了20%的增长,达到6亿
品销售额是2010年A产品销售额的3倍。问2009年B产品的销售额是多少?
A. 0.8亿
B. 1.2亿
C. 1.5亿
D. 2亿
【正确答案】:B
试题解析:
A和B产品的销售额都增长25%,
根据十字交叉法可得到上年这三种产品销售额的比例。

2009年的销售额是6÷(1+20%)=5亿,则C产品占到3亿元,
2010年A产品销售额是1亿元。2009年A产品销售额为1÷(1+25%)=0.8亿元,当年B产品销售额是2-0.8=1.2亿。
第71题 一个袋子里面有10个球,包括红球、白球和黑球。已知从袋中任意摸一个球,得到黑球的概
A. 1
B. 2
C. 3
D. 4
【正确答案】:A
试题解析:
任意摸一个球,
第72题 某保险公司和某顾客签订一份保险合同,假设一年内某顾客投保的事件发生的概率为P,如果事件发生,则公司赔偿顾客y元。若公司在顾客身上的期望收益等于赔偿金y的10%.那么公司应该要求该顾客缴纳的保费为:
A. yp+0.1y
B. y(1-p)+0.1y
C. yp+0.9y
D. y(1-p)+0.9y
【正确答案】:A
试题解析:
期望收益=收取保费一期望支出。期望收益为0.1y,期望支出为py。因此,收取保费=期望收益+期望支出.为yp+0.1y。选A。
第73题 如图,有一个11位数,它的每3个相邻数字之和都是20,则标有*的那个数位上的数字应是几?
A. 9
B. 7
C. 5
D. 3
【正确答案】:B
试题解析:
设这串数为9abcdefghi7,由于“它的每3个相邻数字之和都是20”,可知9+a+b=a+b+c,所以c=9,a+b+C=b+c+d,得到a=d,同理b=e.这串数可以表示为9ab9ab…7,即各位数字以3为周期循环出现,11=3×3+2.所以第二个数等于第十一个数7。第三个数为20-9-7=4,所以这个数为97497497497,标有*的那个数位上的数字是7。
第74题 一个长方体,六个面均涂有红色。沿着长边等距离切5次,沿着宽边等距离切4次,再沿着高边等距离切n次后,若要使各面上均没有红色的小方块为24块,则n的取值是:
A. 2
B. 3
C. 4
D. 5
【正确答案】:B
试题解析:
沿着长边等距离切5次,可以将长方体切成6块;沿着宽边等距离切4次,可以将长方体切成5块;沿着高边等距离切n次后,可以切成n+1块。由题意可知,长方体6个面的外层均涂有红色(小方块上有1面、或2面、或3面涂有红色)。所以,各面均没有红色的小方块共(6-2)×(5-2)×(n+1-2)=12(n-1)=24个。解得n=3。
第75题 小周从家出发骑自行车到公司上班,需要1小时20分。某日小周先到途中的早餐店吃早餐,用去10分钟,然后去公司,结果比平时早到6分钟。6点整下班后,若小周先保持早晨的骑车速度.后半程速度降低20%他将在什么时候到家?
A. 7点20分
B. 7点12分
C. 7点2分
D. 7点之前
【正确答案】:B
试题解析:
这一日小周早晨上班骑车所用时间为80-10-6=64分钟,前半程速度不变,所花时间为64+2=32分钟,后半程速度降低20%,所用时间为32+(1-20%)=40分钟,共用时间32+40=72分钟,所以他将在7点12分到家。
第76题 甲、乙、丙、丁四个人合作加工一批零件,已知四人工作时间相同,甲加工的零件数是其他
工3个零件的时间内,丁只能加工2个。若甲比丁多加工800个零件,问这一批零件有多少个?
A. 2300
B. 3450
C. 4600
D. 4800
【正确答案】:C
试题解析:
假设总的零件数为23份.则甲完成了8份。其余三人完成了15份。由于乙完成的零件数是丙、丁完成零件总数的
4份,比甲少了814:4份,即4份为800个零件,每份为800÷4=200个,总零件数为200×23=4600个。
第77题 某公司每年新增的专利数量呈等比数列.其中第一年获得的专利数量是后两年新增专利数量的六分之一。该公司4个部门每年均有新增专利,且每个部门获得的专利数不相同。则4年间该公司至少新增多少专利?
A. 70项
B. 90项
C. 150项
D. 180项
【正确答案】:C
试题解析:
根据4年来每年新增专利数呈等比数列,令第一年为1,公比为a,则可得a+a2=6,易得a=2。新增专利总数取决于第一年专利数。该公司每个部门新增专利数不相同,则第一年至少有1+2+3+4=10个专利。四年间专利数至少有10+20+40+80=150项。
第78题 某商场6月平均每天卖出某商品50件.已知该月每天都有商品卖出.且每天卖出的商品数各不相同.卖出商品最多的那天比卖出商品最少的那天多卖出70件,问卖出商品不低于50件的最多有多少天?
A. 21
B. 22
C. 23
D. 24
【正确答案】:C
试题解析:
该月卖出商品总数是50×30=1500件。假设最少的那天卖出1件,则最多的那天卖出71件,且(50+71)×22+2=1331,1500-1331=169,满足假设;72+73=145,169-145=24,假设最多的那天卖出73件,最少的那天卖出3件,少于50件大于3件的有5天。且这5天卖出24-3=21件.因为4+5+6+7+8>21,所以不存在:假设最多的那天卖出72件,最少的那天卖出2件,少于50件大于2件的有6天,且这6天卖出169-72-2=95件.因为3+4+5+6+7+8<95.即可以找到6个不同的数的和为95。因此卖出商品不低于50件的最多有23天。本题答案为C。
第79题
理层规定,以后每新进1名男会员,就要同时新进3名女会员,若已有会员保持不变,问当男会员和女会员人数相等时。共有多少名会员?
A. 550
B. 582
C. 592
D. 602
【正确答案】:C
试题解析:
方法一:设原来总会员有×人,
解得×=400.此时男会员
女会员有400-248=152人。设后来新近y名男会员,则248+y=152+3y,解得y=48,即当男会员和女会员人数相等时共有会员(248+48)×2=592人。
开始时总会员人数是8的倍数(也是4的倍数),此后“每新进1名男会员,就要同时新进3名女会员”,则此后新进人数是4的倍数,则最后总人数也是4的倍数,选项中只有C符合。
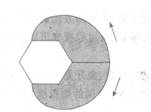
第80题 一个等边六边形的房子一角拴着一条狗,六边形边长为1m,栓狗绳长2m,狗绕着房子行走,绳子最多扫过多少面积?
B.3π
【正确答案】:B
试题解析:
如图所示,绳子以半径为2转过120°,之后扫过的圆半径会缩短为1;再转60°就全绕在
所以绳子最多扫过3π的面积。
温馨提示:因考试政策、内容不断变化与调整,长职理培网站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准! (责任编辑:长职理培)






















点击加载更多评论>>